Foam Cells
The size of foam bubble walls and struts depends mainly on foam's density and average cell size. The app calculates these dimensions from a few easily measurable key foam parameter. It also estimates the mechanical strength of the foam in relation to the strength of the base material from which the foam is made.
Credits
A big Thank You to prof. Steven Abbott for designing and developing the app.
Foam Cells
Foam mechanical properties
//One universal basic required here to get things going once loaded
window.onload = function () {
//restoreDefaultValues(); //Un-comment this if you want to start with defaults
Main();
};
//Main() is hard wired as THE place to start calculating when inputs change
//It does no calculations itself, it merely sets them up, sends off variables, gets results and, if necessary, plots them.
function Main() {
//Save settings every time you calculate, so they're always ready on a reload
saveSettings();
//Send all the inputs as a structured object
//If you need to convert to, say, SI units, do it here!
const inputs = {
// rhorel: sliders.Sliderhorel.value,
phiCell: sliders.SlidephiCell.value, //Everything stays in μm
rhoSolid: sliders.SliderhoSolid.value,
phiFace: sliders.SlidephiFace.value,
Rise: sliders.SlideRise.value,
rhoFoam: sliders.SlideFdens.value, //Foam density input
};
//Send inputs off to CalcIt where the names are instantly available
//Get all the resonses as an object, result
const result = CalcIt(inputs);
//Set all the text box outputs
document.getElementById('rhorel').value = result.rhorel; // relative density calculated
// document.getElementById('rhoFoam').value = result.rhoFoam; // foam density from the slider
document.getElementById('PL').value = result.PL;
document.getElementById('PA').value = result.PA;
document.getElementById('phiStrut').value = result.phiStrut;
document.getElementById('Re').value = result.Re;
document.getElementById('Rf').value = result.Rf;
//document.getElementById('RfRe').value = result.RfRe;
document.getElementById('Ezz').value = result.Ezz+"%";
document.getElementById('Eyy').value = result.Eyy+"%";
document.getElementById('sigmaz').value = result.sigmaz+"%";
document.getElementById('sigmay').value = result.sigmay+"%";
//Do all relevant plots by calling plotIt - if there's no plot, nothing happens
//plotIt is part of the app infrastructure in app.new.js
if (result.plots) {
for (let i = 0; i < result.plots.length; i++) {
plotIt(result.plots[i], result.canvas[i]);
}
}
//You might have some other stuff to do here, but for most apps that's it for Main!
}
//Here's the app calculation
//The inputs are just the names provided - their order in the curly brackets is unimportant!
//By convention the input values are provided with the correct units within Main
function CalcIt({ rhoFoam,phiCell,rhoSolid,phiFace, Rise }) {
const fs=0.8 //A typical value for fraction of struts
//Output foam expansion
const rhorel=rhoFoam/rhoSolid
//Output foam expansion in %
const Prhorel=rhoFoam/rhoSolid*100
//Strut calcs in μm from Glicksman
const Lv=8.6/(phiCell*phiCell) //Length per unit volume
const a=Math.sqrt(fs*rhorel/(0.29*Lv))
const phiStrut=Math.sqrt(4*0.29/Math.PI*a*a)
//Calcs from Abbott Foam Drainage
const e=rhorel //% liquid is just rhorel
const PL=phiCell/2.7 //Length of Plateau border
//const phiStrut=2*PL*Math.sqrt(e/0.17)
const PA=0.785*phiStrut*phiStrut
//const Re=3*PA/(2*1.414*PL*PL)
//Rf weight in facers
//const Rf=18.9*phiFace/(16*PL) //Same as 3*phiFace/phiCell
// Rf % of weight in facers
const Rf=Math.min(100,(18.9*phiFace/(16*PL))*100) //Same as 3*phiFace/phiCell
//old - Re weight in struts Don't allow Re to give super-small or negative values.
//const Re=Math.max(Rf/100,rhorel-Rf)
const Re=100-Rf
//const RfRe=Rf/Re
//Mechanical calcs
const theta=Math.atan(Rise), sin=Math.sin(theta),cos=Math.cos(theta)
const C1=0.1338, C2=1.189, C3=1.149, rt2=Math.sqrt(2), rhoinv=1/rhorel
const X2=2*C2*C3*Math.sqrt(rhorel)*Math.sqrt((8*sin*cos*cos)/(2+rt2*cos))
const Ezz=1/((1-X2)*(1+cos/rt2)*rhoinv+Math.pow(1-X2,3)*Math.pow(2+rt2*cos,2)/(192*Math.pow(sin,3)*C1)*Math.pow(rhoinv,2))
const Eyy=1/((2*(1-X2)+rt2/cos*(1-X2/(rt2*cos)))*(2+rt2*cos)*rhoinv/8 +(sin/Math.pow(cos,4)*Math.pow(1-X2,3)+rt2*Math.pow(1-X2/(rt2*cos),3)/(sin*cos))*Math.pow(2+rt2*cos,2)*rhoinv*rhoinv/(384*C1) )
const sigmaz=1/((1+cos/rt2)*rhoinv+(1-X2)*Math.pow((2+rt2*cos)/sin,1.5)*C2/(8*rt2*C1)*Math.pow(rhoinv,1.5) )
const sigmay=1/((1+cos/rt2)*rhoinv+(1-X2)*(Math.sqrt(sin)*Math.pow(2+rt2*cos,1.5)/(8*rt2*cos*cos)*(C2/C1)*Math.pow(rhoinv,1.5)) )
//Now we return everything - text boxes, plot and the name of the canvas, which is 'canvas' for a single plot
return {
phiStrut: (phiStrut).toFixed(2),
rhorel: (Prhorel).toPrecision(3),
PL:PL.toFixed(2),
PA:PA.toFixed(2),
Rf:Rf.toPrecision(3),
Re:Re.toPrecision(3),
// RfRe:RfRe.toPrecision(3)+" : "+(Re/(Re+Rf)).toFixed(2),
// RfRe:RfRe.toPrecision(3),
Ezz:(Ezz*100).toPrecision(3),
Eyy:(Eyy*100).toPrecision(3),
sigmaz:(sigmaz*100).toPrecision(3),
sigmay:(sigmay*100).toPrecision(3),
};
}
Let's assume you know your cell size, φcell, can estimate the thickness of the cell wall, or face, φface (if you see blue colours in a reflection microscope image, they're 250nm, if green/yellow, they're 300nm . You also know the density of the foam ρFoam and the density of the solid polymer (we can assume that this is the density of the liquid mix before reaction, ρsolid. We can assume that this is the density of the liquid mix before reaction, which for majority of PU formulations is about 1200 kg/m³.
So now you can see the expansion ratio of the foam (expressed as % of solid mass in the foam) followed by calculations of internal dimensions of the foam's cells. If, like most of us, you have difficulty visualising struts etc. explore the 3D version via : Foam-3D
- φStrut: The thickness of the strut (edge or Plateau border)
- LStrut: The length of a typical strut
- AStrut: The cross-sectional area of a strut
- Re: The relative mass of material in the struts
- Rf: The relative mass of material in the faces
The calculations are taken from various sources which often differ in the numerical factors but agree on the general values. In any case, real foams aren't the idealised tetrakaidecahedra often assumed in these calculations. The microscopic photos below show a real closed cell foam under different magnifications.

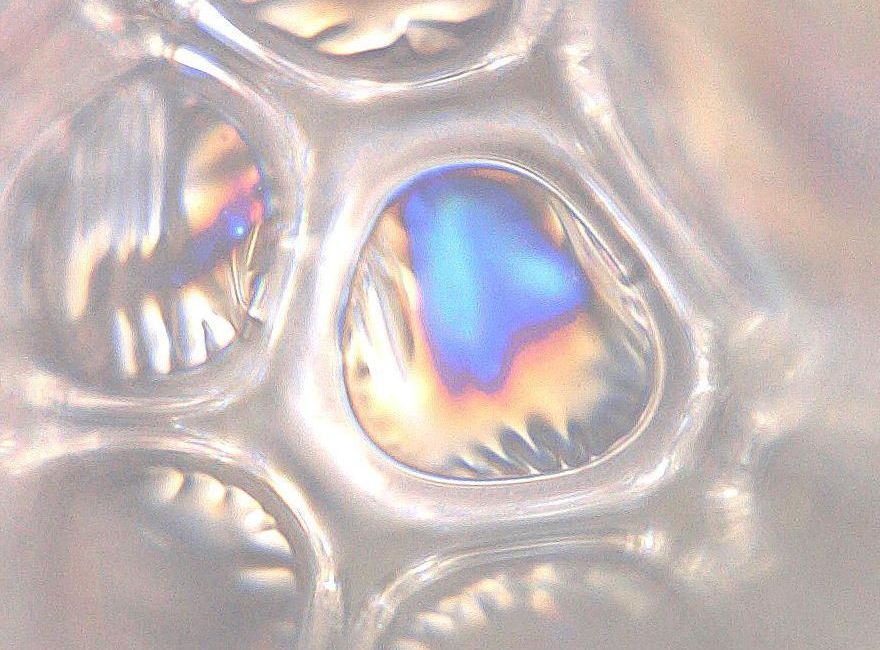

Note that the shape of real life foam cells are much more random, which is the result of combination of many different chemical and physical transformations during the foaming process. You can also see that the walls are very thin in comparison to the struts and nodes. Their thickness is certainly in the nanorange as they defract light creaing this beatifull rainbow effect. The final photo shows real, triangular shape of the strats.
Mechanical properties
An excellent PhD thesis, Muhammad Ridha, Mechanical and Failure Properties of Rigid Polyurethane Foam Under Tension, Nat. U. Singapore, 2007 provides very detailed formulae for the moduli in the z (expansion or rise) direction Ezz and in the y (or x) anti-rise (A-rise) direction Eyy, relative to the properties of the unfoamed PU material. Equations for the tensile stresses, σz and σy are also provided. The equations are far too complex to show here. You can find them in the code and the thesis is freely downloadable.
The thesis explored some geometry options, but the tetrakaidecahedron shape, as in the Foam-3D app happens to give the best fit to the experimental data.
As expected, these values decrease strongly as ρrel becomes low - high expansion foams are much more delicate.
But as the ratio of expansion in the z and y directions gets larger (from 1 for an isotropic foam), the values diverge as those in the z direction increase (because more of the struts are aligned with the load) and those in the y direction decrease (less alignement).